Shader Basics - A Primer On Necessary Mathematics
A lot of the functionality of shaders is dependent on mathematical functions and calculations. Knowing what mathematical functions are useful for various operations is useful for creating visual effects.
There are three main areas of mathematics that are very important to learn and understand:
- Vectors
- Matrices
- Trigonometry
While these aren't the only areas or mathematical concepts used within shaders, they are part of the fundamentals required to understand how and why certain things are done the way they are.
Let's start with going through these main areas of mathematics, and then discuss other needed concepts.
We recommend going through these even if you know about the concepts of these areas, since an explanation into why they're used is also provided.
Vector Mathematics
A vector is generally understood to be an object or piece of data that has a certain amount of magnitude and a direction and shows what it would take to "carry" a point from one position to another.
A vector is made out of multiple components.In 3D vectors, there are three components that store the magnitudes of the vector in the X-axis, Y-axis, and Z-axis, which together provide information about the direction of a vector.
A vector specifically represents a direction from an initial point A to a point B, and the magnitude required to move from the former point to the later.
If we take our initial point as [AsciiMath Syntax:] A = (1, 2, 3) and the final point [AsciiMath Syntax:] B = (3, 5, 8), where the first value is the point location in the X-axis, and the second value is the point location in the Y-axis.
The vector representing moving from the first point to the second would be [AsciiMath Syntax:] vec (AB) = (x_B - x_A, y_B - y_A, z_B - z_A), which is [AsciiMath Syntax:] vec (AB) = (3 - 1, 5 - 2, 8 - 3) = (2, 3, 5)
Vectors are useful as a representation of the data to be processed. Recalling the GPU render pipeline, the first shader stage - the vertex shader - requires data about the vertices of the object which it then operates on.
The most fundamental thing required to be known about a vertex is its position. This can best be represented through vectors.
We know that a vector is data that represents moving a point from one place to another. If the initial point is always the origin [AsciiMath Syntax:] O = (0, 0, 0), then you'll notice that all resulting vectors represent the position of the final point.
The reason for this is quite simple. Every point you plot is always respective to the origin. So when a point is plotted at [AsciiMath Syntax:] A = (1, 2, 3), that point is placed relative to an origin point which is always at [AsciiMath Syntax:] O = (0, 0, 0).
This means that any vector that represents the amount needed to carry the origin to a point will have a value representing that final point.
While points can be used to represent points, they can also be used to represent direction. For example, a vector [AsciiMath Syntax:] vec A = (0, 1, 0) has only a value for the Y-axis. This could be interpreted as some direction that acts along the Y-axis.
Similarly, a vector [AsciiMath Syntax:] vec A = (1, 1, 0) represents a direction that acts along the X-and Y-axis equally. And a vector [AsciiMath Syntax:] vec A = (0.333, 1.0, 0.5) represents a direction that acts fully on the Y-axis, about a half as much on the Z-axis, and only a third as much on the X-axis.
Since vectors can be used to represent both points and directions, a method is required to distinguish between the two. For this, an extra coordinate is added to all vectors, called the [AsciiMath Syntax:] w coordinate.
This means that when a point or direction needs to be represented in a certain number of dimensions, the size of the vector representing it will always be 1 plus the number of dimensions of the point or direction, where the last value is [AsciiMath Syntax:] w.
For points, the value for [AsciiMath Syntax:] w coordinate is always 1, and for directions it's always 0. The reason for this will be discussed in the next section, where we'll talk about matrices.
Matrix Mathematics
Matrices are objects or data that are written as a rectangular array of values. This means that matrices have two dimensions, with data moving vertically and horizontally.
If this is a bit confusing, here is an example of what a matrix looks like:
[AsciiMath Syntax:] a = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
When a particular value in a matrix is being referenced, it is written as [AsciiMath Syntax:] a_(ij), where [AsciiMath Syntax:] i represents the row number, and [AsciiMath Syntax:] j represents the column number.
While vectors are very good at representing data, a method is required to manipulate the data so that transformations can be performed based of the initial vector data provided.
Transformations are essential to calculations since they can change the data into a form that is useful for other calculations. Without transformations, data would always remain fixed within a certain bound, making it less useful.
Let us take a point [AsciiMath Syntax:] a = (1, 2, 3). If we wish to move this point to [AsciiMath Syntax:] b = (7, 3, 5), an operation is required that can "transform" the point [AsciiMath Syntax:] a to point [AsciiMath Syntax:] b.
These sort of transformations are best suited to be done through the use of matrices, which simplify the transformation down into simple multiplication.
The transformations you will generally work with are called linear transformations. To get a basic understanding of what linear transformations are, check out this video by 3Blue1Brown.
Check out this chapter of OpenGL Tutorial to get a basic understanding of matrix mathematics and the linear tranformations required for later chapters, as well as this reference guide by OpenGL Tutorial to learn more about matrix mathematics and some extra additional information on certain linear transformations.
When operating on a point, transformations such as rotating the point around an axis, translating/moving a point, or scaling a point in reference to an origin can be considered valid.
However, with directions, transformations such as translation don't make sense. In order to be able to use the same transformation formulas on both points and directions and make sure that direction vectors are not affected, we can take advantage of the [AsciiMath Syntax:] w component.
By having [AsciiMath Syntax:] w set to 0 for directions, transformations such as translating vectors can be prevented from affecting directions, and only affect points. This section of the third chapter of OpenGL Tutorial provides an example to show this behaviour.
Trigonometry
Similar to matrix mathematics, trigonometry is useful for performing transformations, except that it allows for transformation through the use of regular patterns or shapes.
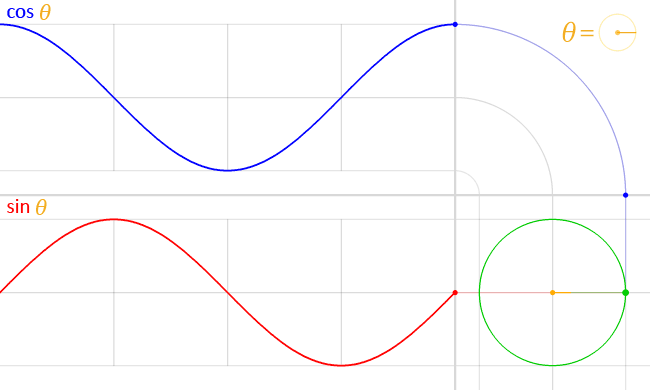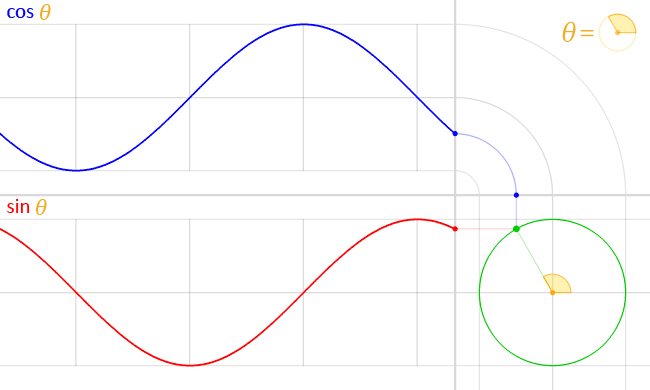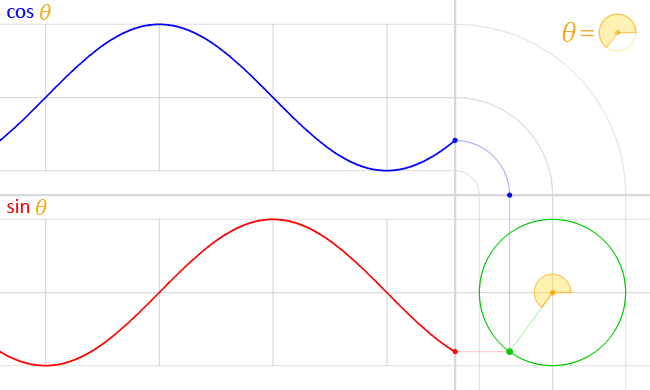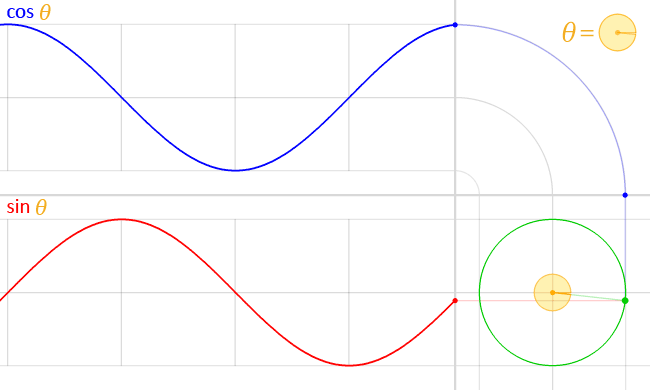
Let's take the example of the trignometric functions [AsciiMath Syntax:] sin(theta) and [AsciiMath Syntax:] cos(theta). These functions, when given a certain angle, produce a certain value between 1 to -1.
If we take [AsciiMath Syntax:] sin(theta), at 0 degrees, it gives the result 0. As the angle increases to 90 degrees, the result of the function becomes 1.
When the angle exceeds 90 degrees and goes to 180 degrees, the result of the function goes back to 0. Further increasing the angle to 270 degrees results in the value decreasing to -1.
Finally, as the angle increases to 360 degrees, the result goes back to 0, resetting the loop. [AsciiMath Syntax:] cos(theta) behaves in a similar way.
Lets visualize what is plotted by these functions on a graph as the angle passed to it keeps increasing.
These functions allow the ability to draw patterns and shapes since the results of these functions draws a line that is continuous and smooth when plotted, allowing for proper transitions and tiles to be drawn through some clever math.
For example, let's take a point [AsciiMath Syntax:] a = (1, 2, 3) which needs animated into being scaled up to double its size, then shrunk down to 0, finally scaled it back to its original size, and then repeating the process.
This can be done by using a scaling transform matrix that uses the value of [AsciiMath Syntax:] cos(theta), where [AsciiMath Syntax:] theta can be the number of seconds that has passed since the start of the animation.
Since the range of values produced by [AsciiMath Syntax:] cos(theta) is between -1 to 1, we can just add 1 to the results to shift the range to 0 to 2, making the equation be [AsciiMath Syntax:] x = cos(theta) + 1.
The scaling transform can then be based upon this value, which would make the matrix be:
[AsciiMath Syntax:] s = [[cos(theta) + 1, 0, 0, 0], [0, cos(theta) + 1, 0, 0], [0, 0, cos(theta) + 1, 0], [0, 0, 0, 1]]
This scaling matrix can then be multiplied with the point to ensure that it is scaled properly based upon the time passed, with the animation being performed by updating the position of the point regularly with the scaling matrix.
Other trignometric functions such as [AsciiMath Syntax:] tan(theta) and [AsciiMath Syntax:] cot(theta) can also be used, although not all trignometric functions (like the aforementioned two) produce continuous lines with increasing angles. This property can still be useful in certain scenarios.
Other Mathematic Concepts
Similar to how trignometric functions can be used to produce patterns and shapes, operations such as [AsciiMath Syntax:] "floor(x)" = floor(x), [AsciiMath Syntax:] "ceil(x)" = ceil(x), [AsciiMath Syntax:] "abs(x)" = abs(x), [AsciiMath Syntax:] "power(x, n)" = x^n, etc. are also useful for the same purpose.
Functions such as these can be referred to as pattern functions or shape functions, since they can help produce patterns and shapes in images.
Summary
- There are three primary areas of math that should be learnt that are used in shader programming:
- Vectors
- Matrices
- Trigonometry
- Vector mathematics is useful for representing data, such as points and directions.
- Matrix mathematics is useful for manipulating data in specific ways, such as moving, rotating, scaling points and directions.
- Trigonometry is useful for manipulating data in specific patterns, such as rotating a point along the circumference of a circle, producing a smooth wave, or generating certain shapes.
- There are other mathematical functions and operations outside of trigonometry that allow for manipulating data in patterns, with each having their own specific properties.